Skip to content

Data-science#

ChatGPT vs Me: As a Children's Authors

For all the right reasons, large language models have taken the world by storm! It’s pretty impressive what ChatGPT can do - unprecedented coherence, relevance and tone of delivery for a synthetic text generation. Well done OpenAI!

I have to admit I have strongly resisted the urge to use it for purposes beyond joy, and exploration. It's been very hard to abstain, especially because I am extremely passionate about AI and also I work in AI. I truly, madly, deeply, utterly fear that we, as a community of carers of young people, are simply NOT ready for it! It’s the infancy state of due diligence to understand the societal implications and governance around it that scares me the most. I fear that while we, the grown-ups, are probably ready and raring to go at it, it’s our younger generations who are not at all ready for it. Once this genie is out of the bottle, out is just the way! And it’s the repeat of our social media fiasco all over again. Perhaps I am coming from a dark place of seeing how exponentially easily our kids are getting social media bullied and exploited with authorities still scrambling even after the fact on how to contain it!

On a lighter note, selfishly speaking, I also fear depleting my creative and critical thinking abilities in favour of convenience and productivity. If Darwin’s theory is anything to go by, that’s one human talent we should preserve and reinforce, I think. Did I hear you say “But you can still be critical of the presented text?”? Sure, but we are also a Large Language Model in many ways :) - we get biased and we are lazy. Is not laziness the inspiration for many useful inventions of our times?

As a mother of young kids and as someone who believes in lifelong learning, I made a tiny effort last year to write chapter books for early readers covering the discoveries of the great scientists of our past and present. In my debut release, I featured Sir Isaac Newton’s discoveries in a book titled “Curious Cassie's beach ride quest: A Celebration of Isaac Newton's Discoveries”. I tested the book on a sample of 5 kids all ranging from 6-7 years and observed extreme enthusiasm and an increased number of questions thereafter. Mission accomplished, eh?

I failed this morning! I failed to resist the chatGPT urge to see what it would write instead. So here’s Me vs chatGPT, a debut author vs a stochastic parrot:

ChatGPT vs Me: Show me the script

ChatGPT

Prompt

Write a chapter book for 6 year old kids

ChatGPT's Response
Chapter 1: The Magical Forest

It was a beautiful day in the magical forest. The sun was shining and the birds were singing. The trees were tall and green, and the flowers were blooming.

In the center of the forest was a small cottage, where a young girl named Lily lived with her parents. Lily was six years old, and she loved to explore the forest.

One day, while out on a walk, Lily stumbled upon a strange and magical place. It was a clearing filled with glittering diamonds and sparkling jewels.

"Wow!" exclaimed Lily. "I've never seen anything like this before!"
As she reached out to touch one of the diamonds, a bright light shone and a magical fairy appeared before her.

"Hello, Lily," said the fairy. "I am the guardian of the forest, and I have been waiting for you. You have a very special task to complete."

"Me?" asked Lily. "What can I do?"

"There is a wicked witch who has been causing trouble in the forest," explained the fairy. "She has been turning all of the animals into stone, and we need your help to stop her."

"I'll do it!" said Lily, determined to help the animals.

Chapter 2: The Wicked Witch

Lily set out on her journey to find the wicked witch. She followed the fairy's instructions and travelled deep into the forest.
As she walked, she saw that the trees were no longer green and the flowers had withered away. It was clear that the witch had been causing destruction wherever she went.

Finally, Lily came to a dark and gloomy castle. She knew this was where the witch lived.

She tiptoed through the castle, trying not to make a sound. She could hear the witch cackling in the next room.

Lily peeked through the door and saw the witch stirring a bubbling pot. She had a long, crooked nose and sharp, pointed teeth.

"Ah-ha!" shouted the witch, turning to face Lily. "I've been expecting you, little girl. You won't be able to stop me from turning all of the animals into stone!"

But Lily was not afraid. She remembered the fairy's words and knew she had to be brave.

"I won't let you harm any more animals!" said Lily, standing up to the witch.

The witch cackled and raised her wand, but Lily was quick. She grabbed a nearby broom and swung it at the witch, knocking the witches wand out of her hand.

The witch let out a cry of rage and fled the castle, leaving Lily to save the animals.

Chapter 3: The Great Celebration

With the witch gone, Lily was able to use her magic to turn the animals back to normal. The forest was filled with joy and celebration.

The fairy thanked Lily for her bravery and offered to grant her one wish.

"I wish for the forest to always be a happy and safe place," said Lily.

The fairy nodded and waved her wand, granting Lily's wish. From then on, the magical forest was filled with happiness and peace.
Lily returned home to her parents, who were overjoyed to see her safe and sound. They threw a great celebration in her honour, and the whole forest came to join in the fun.

Lily knew that she would always treasure her adventure in the magical forest, and she hoped to have many more adventures in the future.
Verdict

Very impressive choice of theme, tone and word selection. It did not give me a title, so I asked to name the title and it responded with "The Brave Explorer: A Magical Adventure in the Forest." Very cool!

Prompt

Write a chapter book for 6 year old kids on STEM

ChatGPT's Response
Chapter 1: The Science Fair

It was a beautiful day in the town of Maplewood, and Lily was excited for the annual science fair at her school. She had been working on her project for weeks, and she couldn't wait to show it off.

Lily's project was a model of the solar system, complete with miniature planets made out of clay and a sun made out of papier-mâché. She had worked hard to make sure everything was accurate and to explain the orbits of the planets in a way that other kids could understand.

As the science fair began, Lily set up her project at her table and waited for the judges to come by. She was a little nervous, but she knew she had done her best.

The judges were impressed by Lily's project and asked her lots of questions about the solar system. Lily was happy to answer and explain what she had learned.

In the end, Lily's project won first place in the science fair! She was so proud of herself and couldn't wait to show her parents.

Chapter 2: The Technology Club

After the science fair, Lily's teacher, Mrs. Kim, asked her if she would like to join the Technology Club at school. Lily was excited at the chance to learn more about science and technology, and she eagerly accepted.

In the Technology Club, Lily and her friends learned about all sorts of different topics, from coding and robotics to engineering and renewable energy. They built and programmed robots, designed and tested bridges, and learned about how solar panels work.

Lily loved the Technology Club and couldn't wait to go each week. She learned so much and had a lot of fun doing it.

Chapter 3: The Engineering Competition

One day, Mrs. Kim announced that the Technology Club was going to participate in an engineering competition. The students would have to design and build a Rube Goldberg machine, a complicated contraption that could perform a simple task in a creative and convoluted way.

Lily and her friends were up for the challenge and set to work planning and building their machine. They worked together as a team, using their knowledge of physics, engineering, and problem-solving to make their machine work.

Finally, the day of the competition arrived. Lily and her friends were nervous but excited to see how their machine would perform.

As they presented their machine to the judges, it worked perfectly, performing the simple task with a series of intricate steps. Lily and her friends were thrilled when they were announced as the winners of the competition!

Chapter 4: The Future Scientists

After the engineering competition, Lily and her friends in the Technology Club knew that they wanted to continue exploring science and technology in the future. They were already thinking about new projects and competitions they could participate in.

Lily knew that she wanted to be a scientist when she grew up, and she was grateful for all of the opportunities she had had to learn and explore in the Technology Club.

She knew that no matter what she did in the future, she would always have a passion for science and technology and the desire to learn more.
Verdict

Nice plot setting, nice choice of theme, and context. Nice job. I find it's very peripheral, explaining a lot about the setting but nothing about science. Maybe it’s my prompt. Let's give it another go.

Prompt

Write a 6-7 year old kids’ book on Sir Isaac Newton's discoveries with Cassie as a protagonist

ChatGPT's Response
Cassie and the Apple Tree

Cassie was a curious little girl who loved to learn about the world around her. One day, she was walking through her backyard when she saw an apple fall from a tree.

"Hmm, I wonder why that happened?" Cassie thought to herself. She climbed up the tree to see if she could find out more.

As she reached the top, she saw a man standing under the tree. It was Sir Isaac Newton! Cassie had heard of him before. He was a very smart man who had made many important discoveries.
"Hello, Cassie," Sir Isaac said. "I see you're curious about the apple."

"Yes, I am," Cassie replied. "Why did it fall to the ground?"
"Ah, that's a good question," Sir Isaac said. "I figured out that there is a force called gravity that pulls objects towards the ground. That's why the apple fell."

Cassie was amazed. "Wow, that's so cool!" she exclaimed.
Sir Isaac smiled. "I also made many other discoveries," he told Cassie. "Like the laws of motion, which explain how objects move and change speed. And I invented calculus, which helps us understand how things change over time."

Cassie's head was spinning with all this new information. She couldn't wait to learn more about Sir Isaac's discoveries.

"Thank you for telling me all about this, Sir Isaac," Cassie said. "I can't wait to learn more!"

"You're welcome, Cassie," Sir Isaac replied. "I'm glad you're interested in learning. Remember, the more you learn, the more you'll discover about the world around you."

Cassie smiled and climbed back down the tree, excited to keep learning and discovering new things.
Verdict

Nice choice of words, context is spot on, and tone of delivery is nice too. Some of the phrases are spot on. "Wow, that's so cool!" she exclaimed.” is something I have used too.

Apple and Newton are joined together forever. Cliché, my dear parrot! Cliché! Well done still. Maybe I like more challenges given to the kids, but I still feel it’s too shallow and lacks details. Let’s give it more work and see what ChatGPT does.

Prompt

Write a 6-7 year old kids chapter book on Sir Isaac Newton's discoveries with Cassie as the protagonist with illustrations

ChatGPT's Response
Chapter 1: Cassie and the Apple Tree

[Illustration: Cassie is standing in her backyard, looking up at an apple falling from a tree.]

Cassie was a curious little girl who loved to learn about the world around her. One day, she was walking through her backyard when she saw an apple fall from a tree.

"Hmm, I wonder why that happened?" Cassie thought to herself. She climbed up the tree to see if she could find out more.

[Illustration: Cassie is climbing up the tree, with a determined look on her face.]

As she reached the top, she saw a man standing under the tree. It was Sir Isaac Newton! Cassie had heard of him before. He was a very smart man who had made many important discoveries.

"Hello, Cassie," Sir Isaac said. "I see you're curious about the apple."

"Yes, I am," Cassie replied. "Why did it fall to the ground?"

"Ah, that's a good question," Sir Isaac said. "I figured out that there is a force called gravity that pulls objects towards the ground. That's why the apple fell."

[Illustration: Sir Isaac is pointing to a diagram of the earth and the apple, with an arrow labeled "gravity" pointing from the earth to the apple.]

Cassie was amazed. "Wow, that's so cool!" she exclaimed.

Chapter 2: The Laws of Motion

After learning about gravity, Cassie couldn't wait to find out more about Sir Isaac's discoveries. She asked him to tell her more.

"I also made many other discoveries," Sir Isaac said. "Like the laws of motion, which explain how objects move and change speed."

[Illustration: Sir Isaac is holding a book labeled "Laws of Motion," with diagrams of moving objects in the background.]

Cassie was fascinated. Sir Isaac explained that there are three laws of motion:

    Objects at rest stay at rest, and objects in motion stay in motion with the same speed and direction, unless acted upon by a force.
    The force needed to change the motion of an object is equal to the mass of the object times its acceleration.
    For every action, there is an equal and opposite reaction.

[Illustration: Sir Isaac is pointing to a chalkboard with the three laws of motion written on it, with illustrations of objects in motion on either side.]

"These laws help us understand how objects move and behave in the world around us," Sir Isaac said.

Chapter 3: Calculus

Cassie couldn't believe how much she was learning from Sir Isaac. She asked him if there was anything else he had discovered.

"Yes, I also invented calculus," Sir Isaac said. "It helps us understand how things change over time."

[Illustration: Sir Isaac is holding a book labeled "Calculus," with a diagram of a curve on the cover.]

Cassie was a little confused. "What do you mean?" she asked.

Sir Isaac explained that calculus is a way of studying how things change. "For example, we can use calculus to understand how fast a ball is rolling down a hill, or how fast a plant is growing," he said.
[Illustration: Sir Isaac is pointing to a graph with a curve on it, with a ball rolling down a hill in the background.]
Cassie was amazed. "That's so cool!" she exclaimed.
Chapter 4: The End
After learning all about Sir Isaac's discoveries, Cassie was even more excited to keep learning and discovering new things. She thanked Sir Isaac for all of his help and said goodbye.
"Remember, Cassie," Sir Isaac said as she walked away. "The more you learn, the more you'll discover about the world around you."
[Illustration: Cassie is waving goodbye to Sir Isaac, with a big smile on her face.]
Cassie smiled and waved, excited to keep exploring and learning. She knew that there were so many more mysteries to solve and discoveries to be made.
Verdict

I love this line "The more you learn, the more you'll discover about the world around you." ChatGPT, You can be nice if not exploited! I liked the mention of calculus. It’s a brilliant thought but I stopped at algebra in my book!

However, I remain unsatisfied given the lack of detail and meat around the topic. I feel, for now, human writing is more creative, rich and informative! I am glad that’s the way it is!

Me! Me!

Title: Curious Cassie's beach ride quest: A Celebration of Isaac Newton's Discoveries

[Illustration: Cassie is riding in a car with her family! She is buzzing with interesting curious keywords like Wow, What, How, When, Where! Sir Isaac is featured in the book.]

Here's a sample of my book. It shows 1st chapter of the 3-chapter book.

I am just a debut author, writing out of hobby. I am profoundly impressed by authors who have written brilliant books to teach, guide and shape our children. I hope we will continue to create far-enriched content to shape ourselves and our future with or without AI - just as long as we are in control.

Thanks a lot for reading! If you ever see any value in spreading the word about my book or procuring it for your loved ones then please do so, I would be thrilled!

Disclaimer: This is a personal post. Views shared are my own and do not represent my employers.

Review and comparison of two manifold learning algorithms: t-SNE and UMAP

What are manifold learning algorithms? What is t-SNE and UMAP? What are the differences between t-SNE and UMAP? How can I explore the features of a dataset using t-SNE and UMAP? These are my notes from my recent exploration into t-SNE and UMAP and trying to apply them to a multi-label dataset to understand the abilities and limits of these algorithms.

This post is broken down into the following sections:

Manifold learning algorithms (MLA)

For us humans, high-dimensional data are very difficult to visualize and reason with. That's why we use dimensionality reduction techniques to reduce data dimensions so that the data is easy to work with and reason about. Manifold learning algorithms (MLA) are dimensionality reduction techniques that are sensitive to non-linear structures in data. The non-linearity is what sets manifold learning apart from other popular linear dimensionality reduction techniques like Principal Component Analysis (PCA) or Independent Component Analysis (ICA). Non-linearity allows MLAs to retain complex and interesting properties of data that would otherwise be lost in linear reduction/projection. Because of this property, MLA is a very handy algorithm to analyze data - to reduce data dimensions to 2D or 3D, and visualize and explore them to find patterns in datasets.

t-SNE (t-Distributed Stochastic Neighbor Embedding) and Uniform Manifold Approximation and Projection UMAP are the two examples of MLA, that I will cover in this post. I will compare and contrast them and provide a good intuition of how they work and how to choose one over the other.

Note that, MLAs are tweaks and generalizations of existing linear dimensionality reduction frameworks themselves. Similar to linear dimensionality reduction techniques, MLAs are predominantly unsupervised even though supervised variants exist. The scope of this post is unsupervised techniques, however.

So what does non-linearity buys us? The following shows the difference in reduction using PCA vs t-SNE, as shown in McInnes excellent talk:

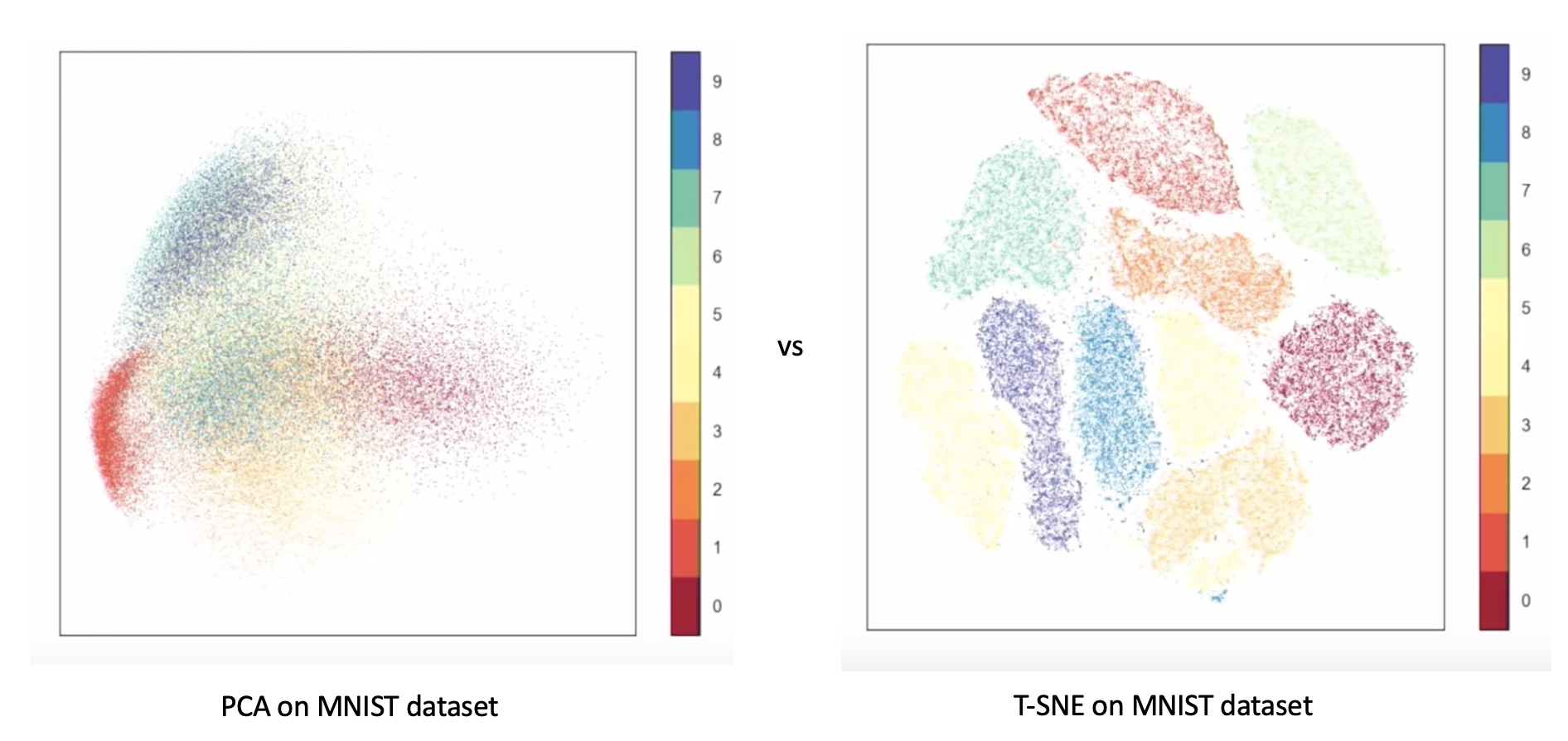Comparison of t-SNE and UMAP on MNIST dataset. (Image from McInnes talk)

As we can see, PCA retains some structure. However, it is very well pronounced in t-SNE, and clusters are more clearly separated.

Neighbour graphs

t-SNE and UMAP are neighbor graph technique that models data points as nodes, with weighted edges representing the distance between the nodes. Through various optimizations and iterations, this graph and layout are tuned to best represent the data as the distance is derived from the "closeness" of the features of the data itself. This graph is then projected on reduced dimensional space a.k.a. embedded space. This is a very different technique than matrix factorization as employed by PCA, ICA for example.

t-Distributed Stochastic Neighbor Embedding (t-SNE)

t-SNE uses Gaussian joint probability measures to estimate the pairwise distances between the data points in the original dimension. Similarly, the student's t-distribution is used to estimate the pairwise distances between the data points in the embedded space (i.e. lower dimension or target dimension). t-SNE then uses the gradient descent technique to minimize the divergence between the two distributions in original and embedded space using the Kullback-Leibler (KL) divergence technique.

Perplexity in t-SNE is effectively the number of nearest neighbors considered in producing the conditional probability measure. A larger perplexity may obscure small structures in the dataset while small perplexity will result in very localized output ignoring global information. Perplexity must be less than the size of data (number of data points) then; otherwise, we are looking at getting a blobby mass. The recommended range for perplexity lies between 5-50, with a more general rule that the larger the data, the larger the perplexity.

Because of the use of KL divergence, t-SNE preserves the local structure in the original space, however, global structure preservation is not guaranteed. Having said that, when initialization with PCA is applied, the global structure is somewhat preserved.

Talking more about structures, the scale of distances between points in the embedded space is not uniform in t-SNE as t-SNE uses varying distance scales. That's why it is recommended to explore data under different configurations to tease out patterns in the dataset. Learning rate and number of iterations are two additional parameters that help with refining the descent to reveal structures in the dataset in the embedded space. As highlighted in this great distill article on t-SNE, more than one plot may be needed to understand the structures of the dataset.

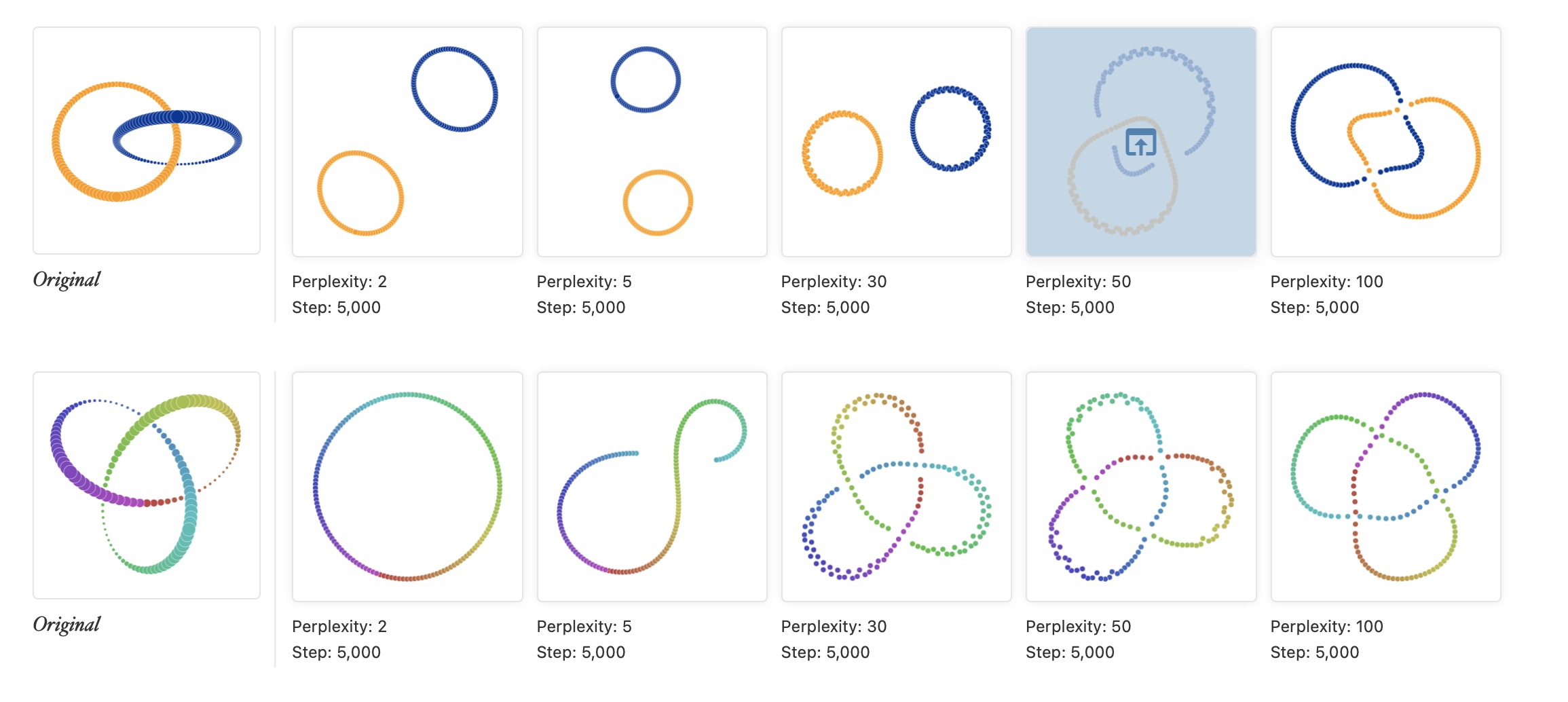Different patterns are revealed under different t-SNE configurations, as shown by distill article. (Image from distill).

t-SNE is known to be very slow with the order of complexity given by O(dN^2) where d is the number of output dimensions and N is the number of samples. Barnes-Hut variation of t-SNE improves the performance [O(dN log N)] however Barnes-Hut can only work with dense datasets and provide at most 3d embedding space. The efficiency gain in Barnes-Hut is coming from changes in gradient calculation which are done with O(n log n) complexity, that uses approximation techniques which leads to about 3% error in nearest neighbor calculation.

Because of these performance implications, a common recommendation is to use PCA to reduce the dimension before applying t-SNE. This should be considered very carefully especially if the point of using t-SNE was to explore into non-linearity of the dataset. Pre-processing with linear techniques like PCA will destroy non-linear structures if present.

Uniform Manifold Approximation and Projection UMAP

UMAP is based on pure combinatorial mathematics that is well covered in the paper and is also well explained by author McInnes in his talk and library documentation is pretty well written too. Similar to t-SNE, UMAP is also a topological neighbor graph modeling technique. There are several differences b/w t-SNE and UMAP with the main one being that UMAP retains not only local but global structure in the data.

There is a great post that goes into detail about how UMAP works. High level, UMAP uses combinatorial topological modeling with the help of simplices to capture the data and applies Riemannian metrics to enforce the uniformity in the distribution. Fuzzy logic is also applied to the graph to adjust the probability distance if the radius grows. Once the graphs are built then optimization techniques are applied to make the embedded space graph very similar to the original space one. UMAP uses binary cross-entropy as a cost function and stochastic gradient descent to iterate on the graph for embedded space. Both t-SNE and UMAP use the same framework to achieve manifold projections however implementation details vary. Oskolkov's post covers in great detail the nuances of both the techniques and is an excellent read.

UMAP is faster for several reasons, mainly, it uses random projection trees and nearest neighbor descent to find approximate neighbors quickly. As shown in the figure below, similar to t-SNE, UMAP also varies the distance density in the embedded space.

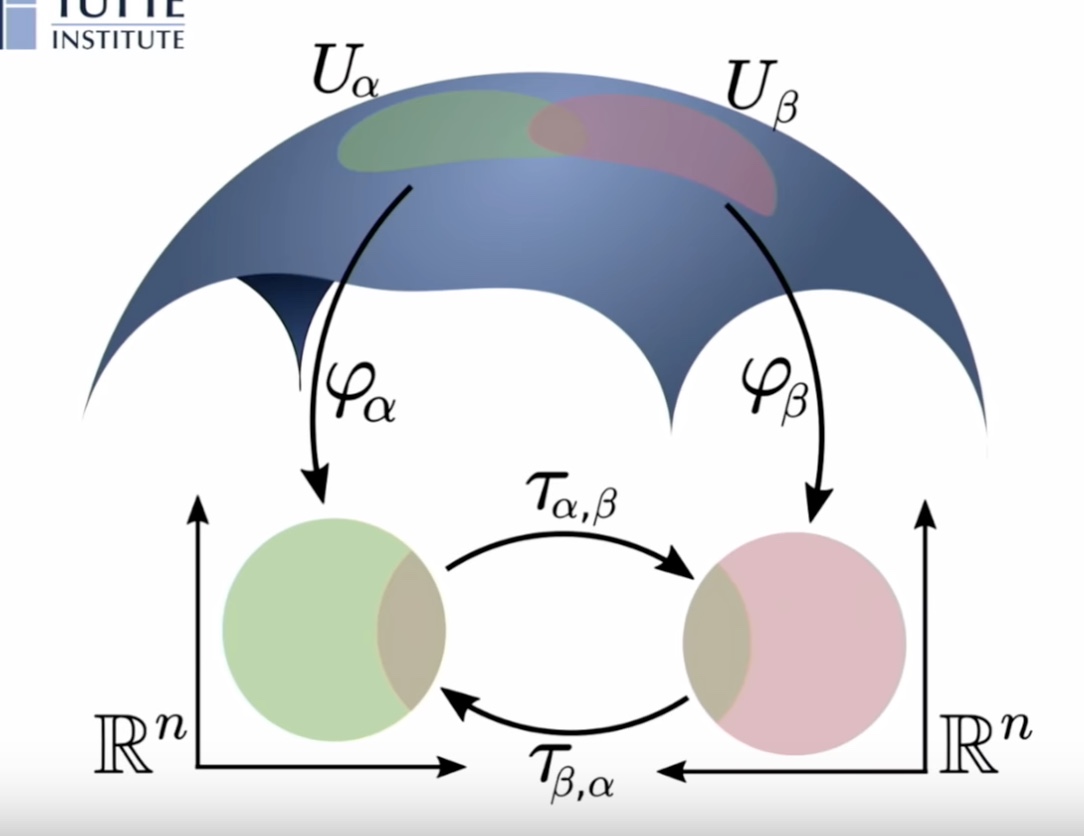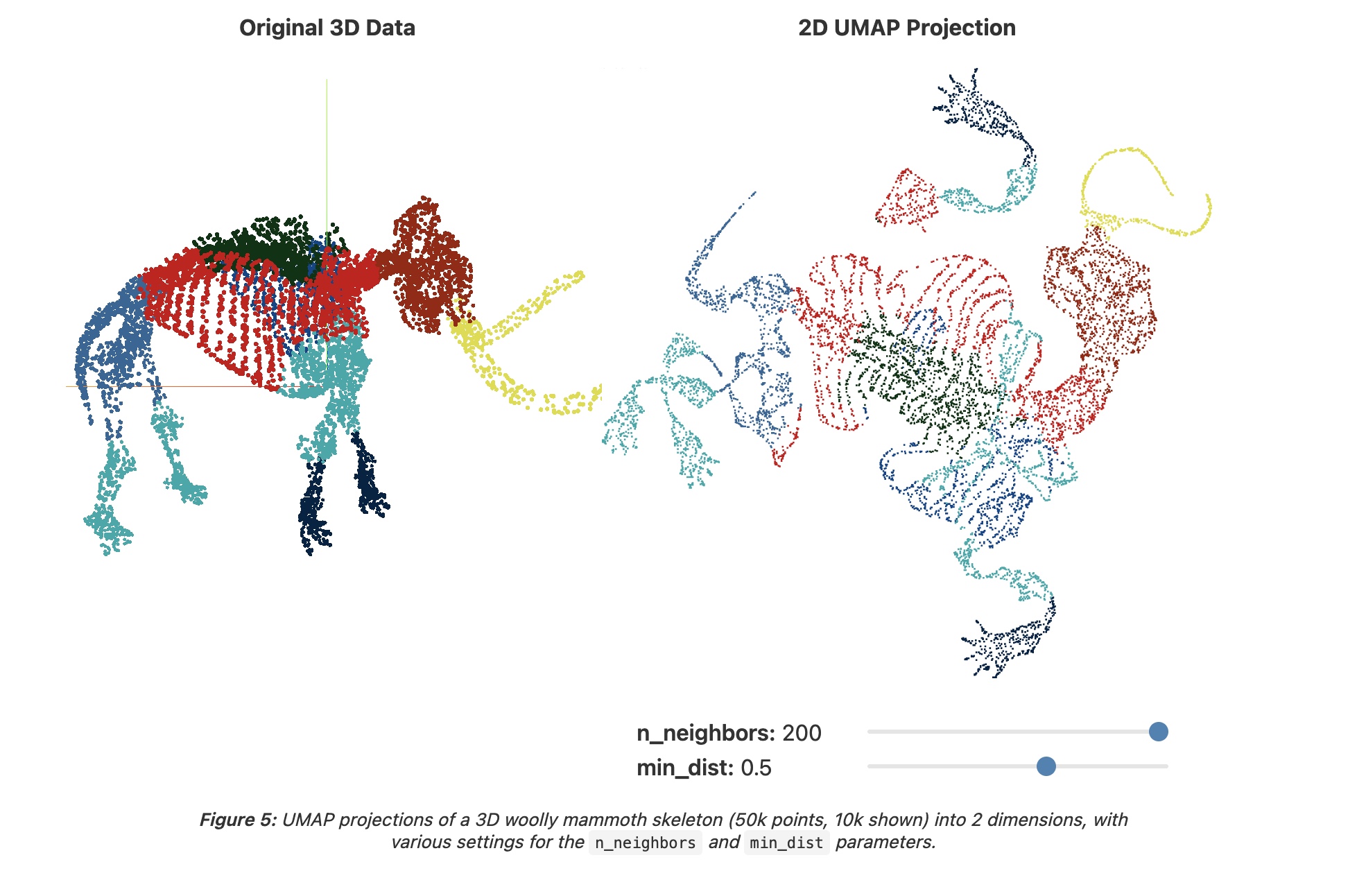Manifold reprojection used by UMAP, as presented by McInnes in his talk. (Image from McInnes talk)

Here's an example of UMAP retaining both local and global structure in embedded space:

Example of UMAP reprojecting a point-cloud mammoth structure on 2-D space. (Image provided by the author, produced using tool 1)

Here's a side-by-side comparison of t-SNE and UMAP on reducing the dimensionality of a mammoth. As shown, UMAP retains the global structure but it's not that well retained by t-SNE.

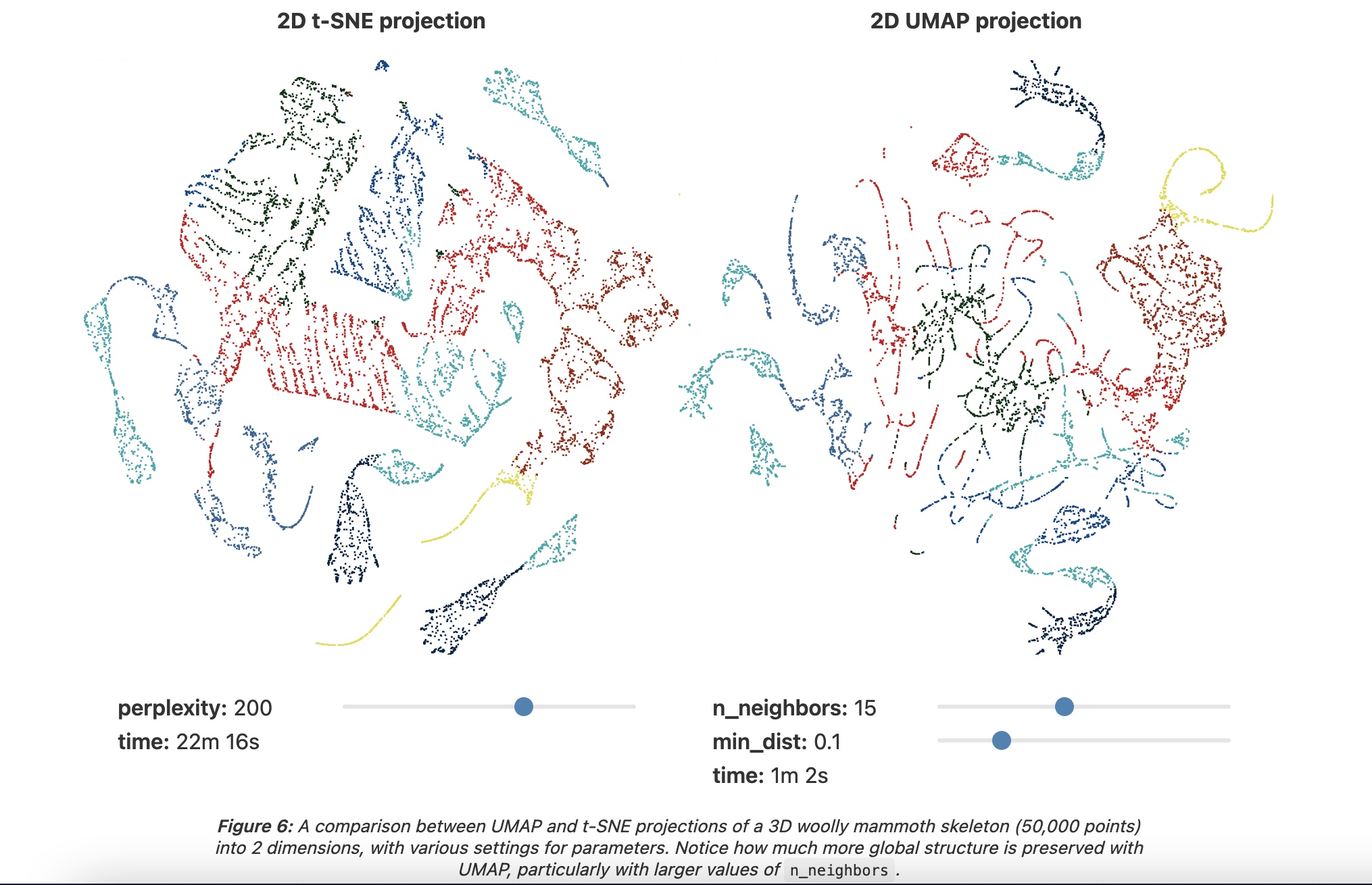Side by side comparison of t-SNE and UMAP projections of the mammoth data used in the previous figure. (Image provided by the author, produced using tool 1)

The explanation for this difference lies in the loss function. As shown in the following figure, UMAP uses binary cross-entropy that penalizes both local (clumps) and global (gaps) structures. In t-SNE however, due to KL Divergence as the choice of the cost function, the focus remains on getting the clumps i.e. local structure right.

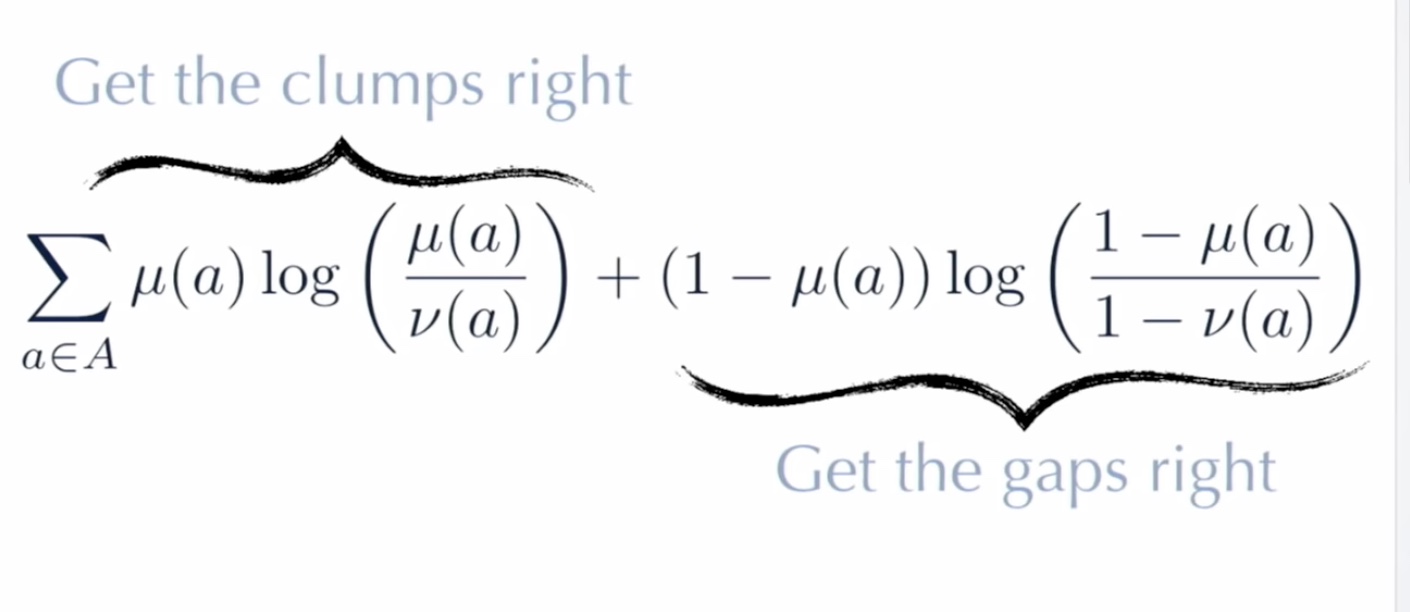Cots function used in UMAP as discussed in McInnes talk. (Image from McInnes talk)

The first part of the equation is the same in both t-SNE (coming from KL divergence) and UMAP. UMAP only has the second part that contributes to getting the gaps right i.e. getting the global structure right.

Comparison table: t-SNE vs UMAP

Characteristics t-SNE UMAP
Computational complexity O(dN^2)
(Barnes-Hut with O(dN log N) )		 O(d*n^1.14)
(emprical-estimates O(dN log N))
Local structure preservation Y Y
Global structure preservation N
(somewhat when init=PCA)		 Y
Cost Function KL Divergence Cross Entropy
Initialization Random
(PCA as alternate)		 Graph Laplacian
Optimization algorithm Gradient Descent (GD) Stochastic Gradient Descent (SGD)
Distribution for modelling distance probabilities Student's t-distribution family of curves (1+a*y(2b))-1
Nearest neighbors hyperparameter 2^Shannon entropy nearest neighbor k

Exploring dataset with t-SNE & UMAP

Now that we have covered theoretical differences, let's apply these techniques to a few datasets and do a few side-by-side comparisons between t-SNE and UMAP.

Source code and other content used in this exercise are available in this git repository - feature_analysis. The notebook for MNIST analysis is available here. Likewise, the notebook for CIFAR analysis is available here.

Simple feature dataset like MNIST

The following figure reprojects MNIST image features on the 2D embedded space under different perplexity settings. As shown, increasing the perplexity, makes the local clusters very packed together. In this case, PCA based initialization technique was chosen because I want to retain the global structure as much as possible.

Reprojection of MNIST image features on the 2D embedded space using t-SNE under different perplexity settings. (Image provided by author)

It's quite interesting to see that the digits that are packed close together are: 1. 7,9,4 2. 3,5,8 3. 6 & 0 4. 1 & 2 5. That 6 is more close to 5 than 1 6. Likewise 7 is closer to 1 than 0.

At a high level this co-relation makes sense, the features of the digits that are quite similar are more closely packed than digitals that are very different. Its also, interesting to note that 8 and 9 have anomalies that map closely to 0 in rare cases in embedded space. So what's going on? Following image overlays randomly selected images on the clusters produced by t-SNE @ perplexity of 50.

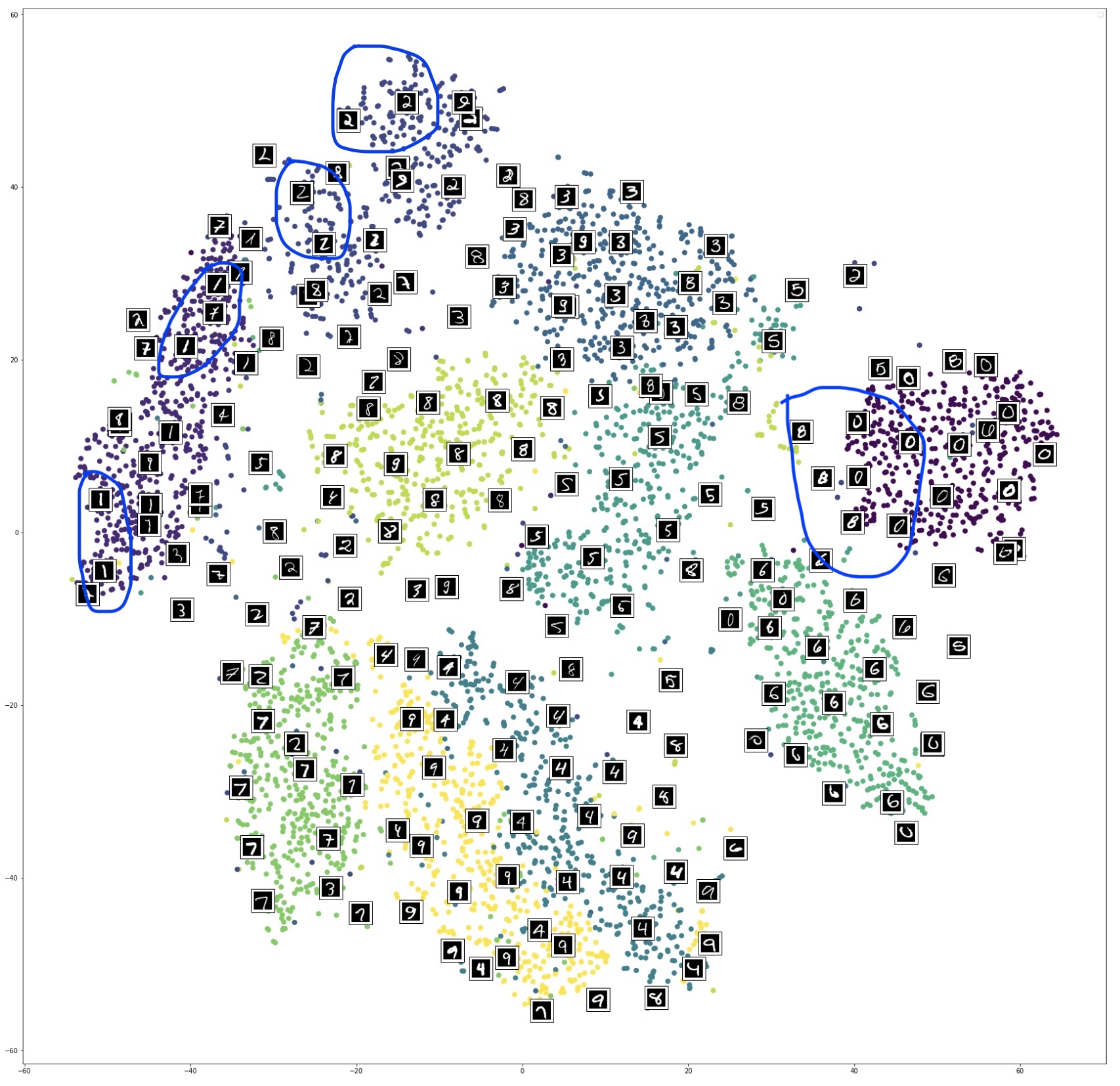Reprojection of MNIST image features on the 2D embedded space using t-SNE @ perplexity=50 with randomly selected image overlay. (Image provided by author)

As we pan around this image, we can see a distinct shift in the characteristics of the digits. For example, the 2 digits at the top are very cursive and have a round little circle at the joint of the two whereas as we travel to the lower part of the cluster of 2s, we can see how sharply written the bottom 2s are. The bottom 2s features are sharp angular joints. Likewise, the top part of the cluster of 1s is quite slanty whereas the bottom 1s are upright.

It's quite interesting to see that the 8's occasionally clustered together with 0's are quite round in the middle and do not have the sharp joint in the middle.

So, what does MNIST data look like with UMAP? UMAP's embedded space also reflects the same grouping as discussed above. In fact, UMAP and t-SNE clustering in terms of digits grouping are very much alike. It appears to me that UMAP and t-SNE are mirror reflections when it comes to how digits are grouped.

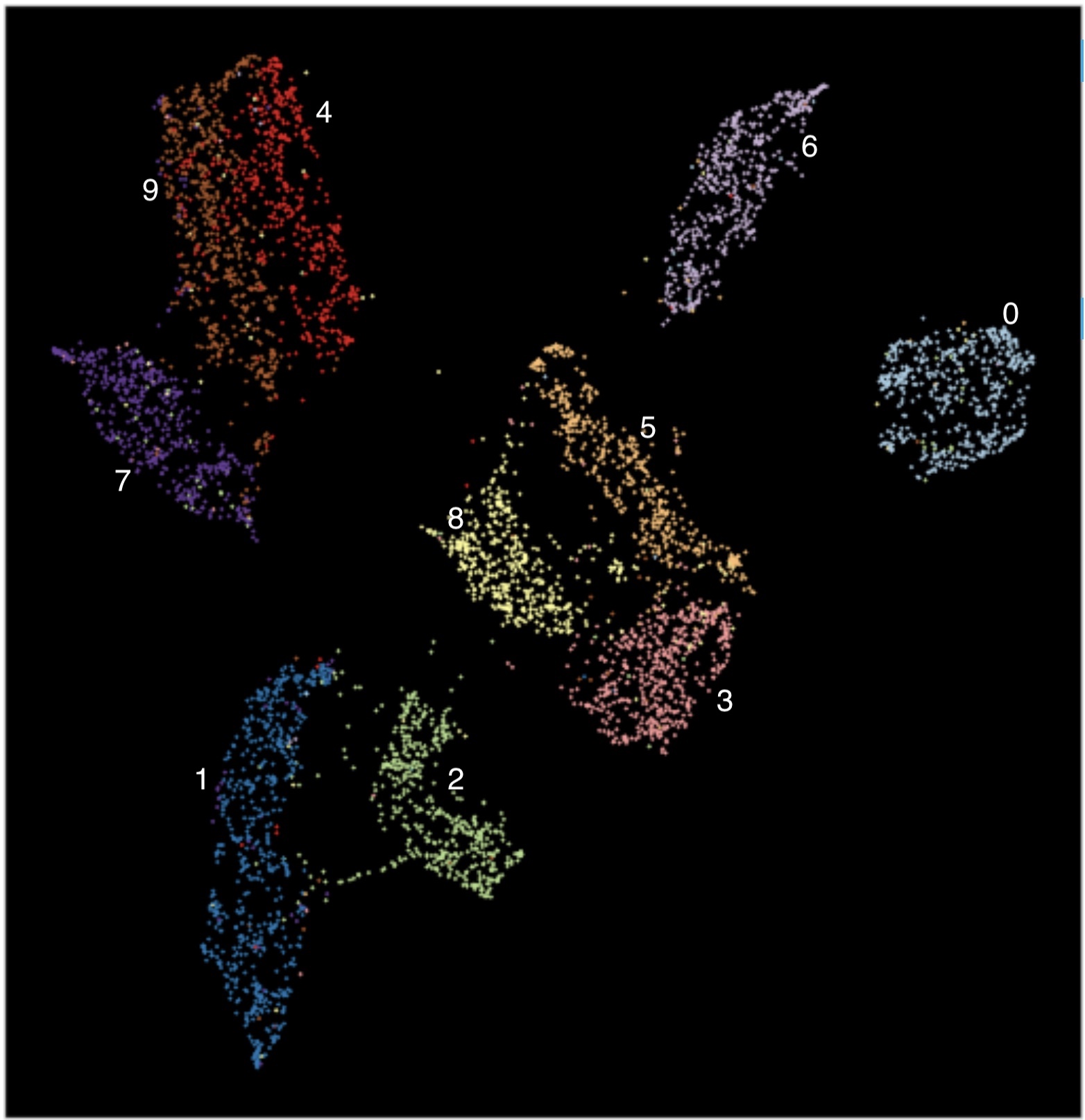Reprojection of MNIST image features on the 2D embedded space using UMAP. (Image provided by author)

It's also very interesting to note how similar-looking 1s are that are reprojected to the same coordinates in the embedded space.

One example of samples that get reprojected to the same coordinates in the embedded space using UMAP. (Image provided by author)

Not all the data points that collide in embedded space will look exactly similar, the similarity is more in the reduced dimensional space. One such example is shown below. Here 1 and 0 are reprojected to the same coordinates. As we can see the strokes on the left side of 0 are very similar to strokes of 1. The circle of zero is not quite complete either.

One example of two different digits getting reprojected to the same coordinates in the embedded space using UMAP. (Image provided by author)

Here's also an example of samples falling into the same neighborhood in the embedded space that look quite distinct despite sharing some commonality (the strokes around the mouth of 4 and incomplete 8s)!

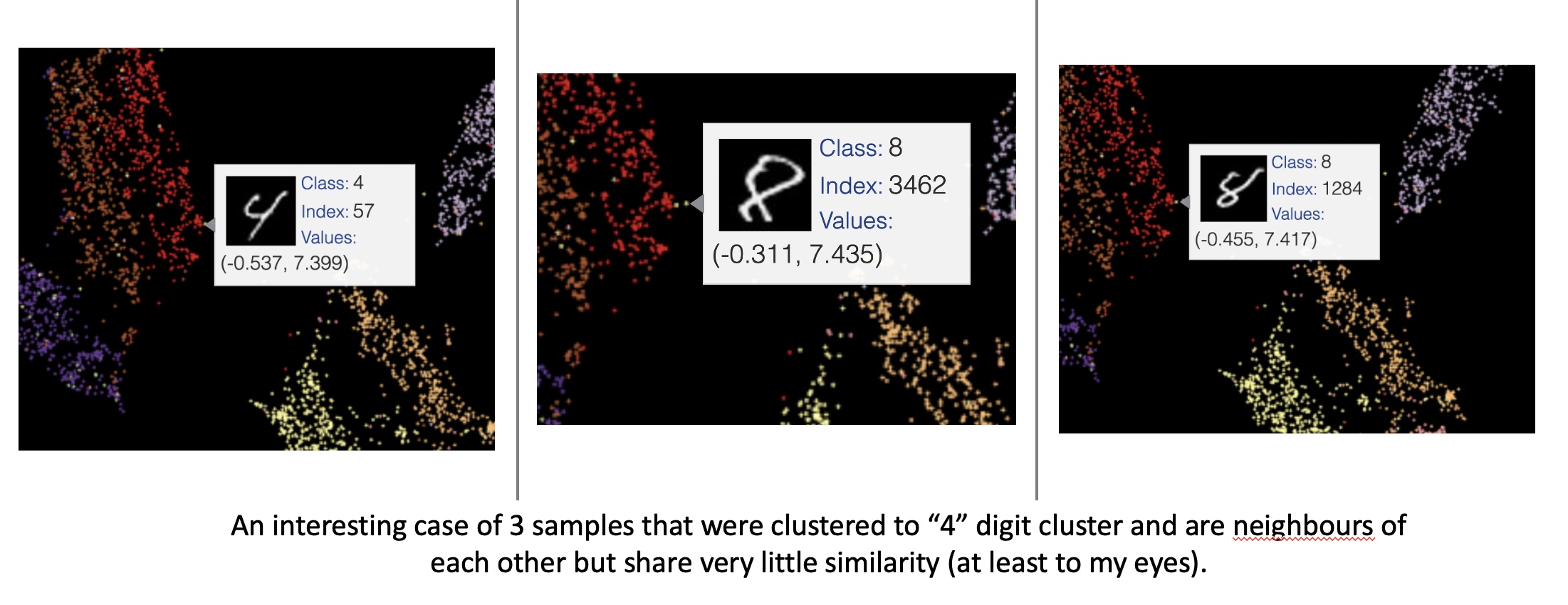Example of 4 and 8s reprojected to the nearby coordinates in the embedded space using UMAP. (Image provided by author)

Its unpredictable what tangible features have been leveraged to calculate the similarities amongst data points in the embedded space. This is because the main focus of MLAs has been distance measures and the embedded space is derived based on best effort using unsupervised techniques with evident data loss (due to dimensionality reduction).

This was MNIST, where digits are captured with empty backgrounds. These are very easy cases because all the signals in the feature vectors are true signals that correspond to the digit as its drawn. When we start talking about visualizing data where there are noises in the signals then that case poses certain challenges. For example, taking the case of cifar dataset, the images of things are captured with a varying background as they are all-natural images unlike MNIST with a black background. In the following section, let's have a look at what happens when we apply t-SNE and UMA to the CIFAR dataset.

High-level differences between cifar and MNIST dataset. (Image provided by author)

More complex datasets like CIFAR

The following figure shows the resultant embedding of CIFAR images after applying UMAP. As shown below results are less than impressive to delineate amongst CIFAR classes or perform any sort of features analysis.

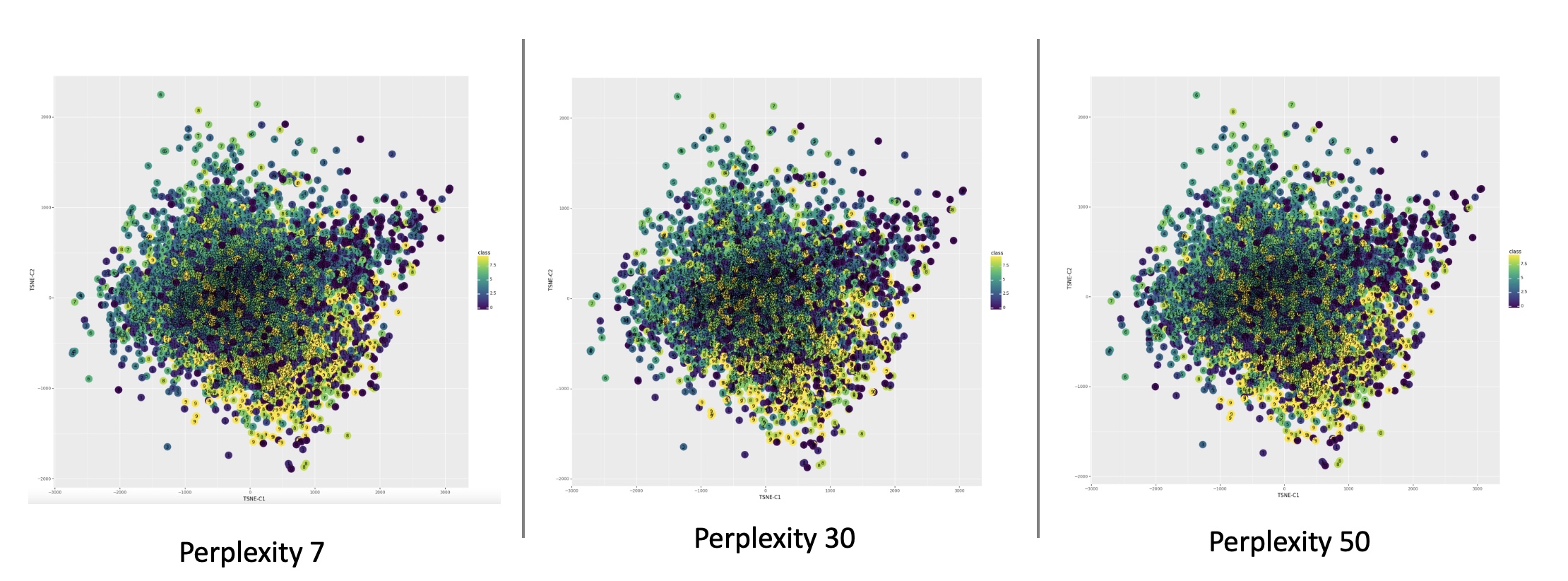Results of CIFAR image feature visualization using t-SNE under different perplexity settings. (Image provided by author)

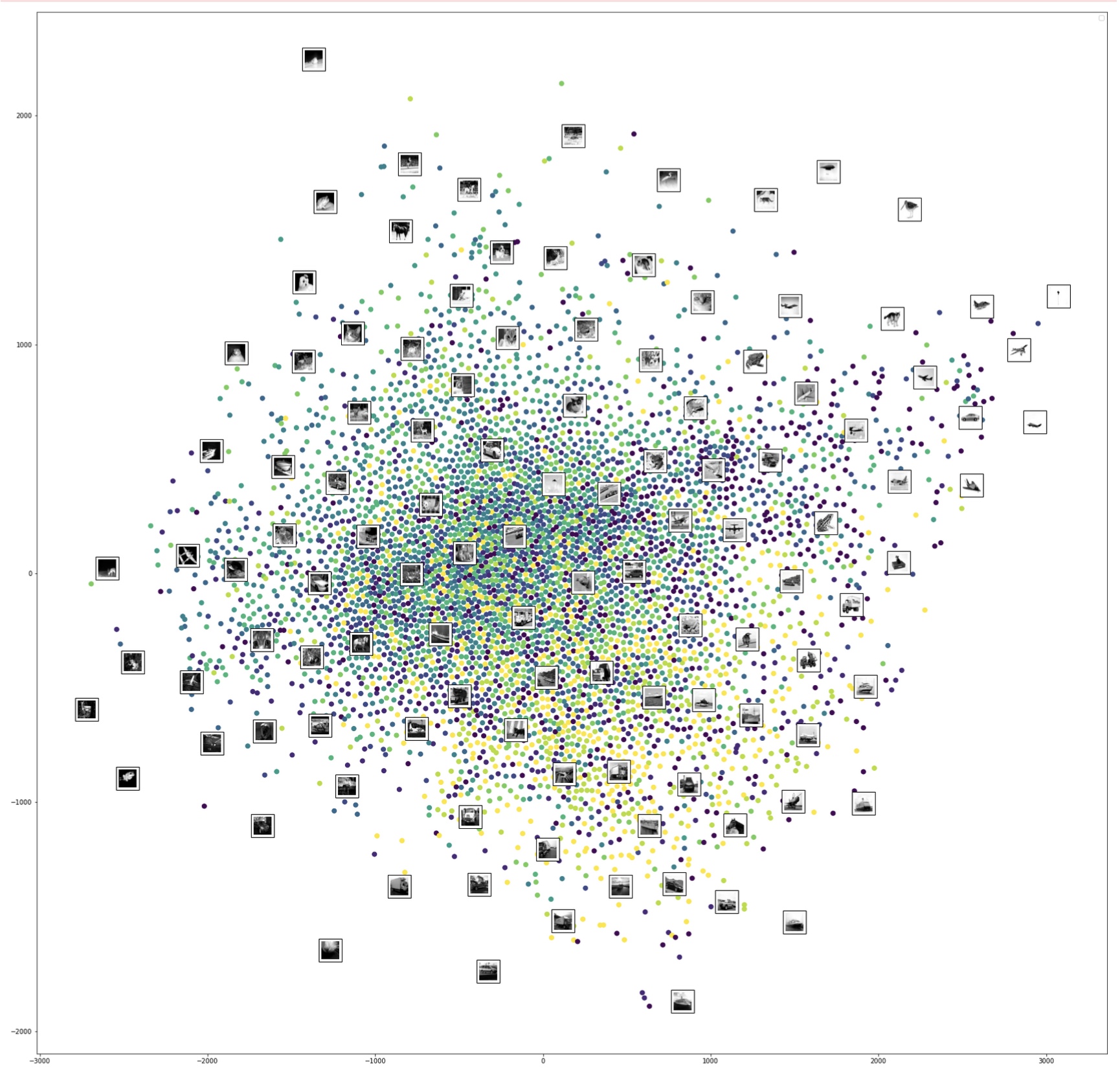So, what's going on? Let's overlay the images and see if we can find some patterns and make sense of the one big lump we are seeing. The following figure overlays the image. It's really hard to find a consistent similarity between neighboring points. Often we see cars and vehicles nearby but not consistently. They are intermixed with flowers and other classes. It's simply too much noise in the feature vector to do any meaningful convergence.

Results of CIFAR image feature visualization using t-SNE. Shows images in an overlay on randomly selected points. (Image provided by author)

In the above two figures, we looked at analyzing CIFAR with t-SNE. The following plot is produced by using UMAP. As we can see it's not convincing either. Much like t-SNE, UMAP is also providing one big lump and no meaningful insights.

Results of CIFAR image feature visualization using UMAP. (Image provided by author)

Following show images of 2 cats that are projected to the same location in embedded space. There is some similarity between the two images like nose, and sharp ears obviously but also the two images have varying distinct features.

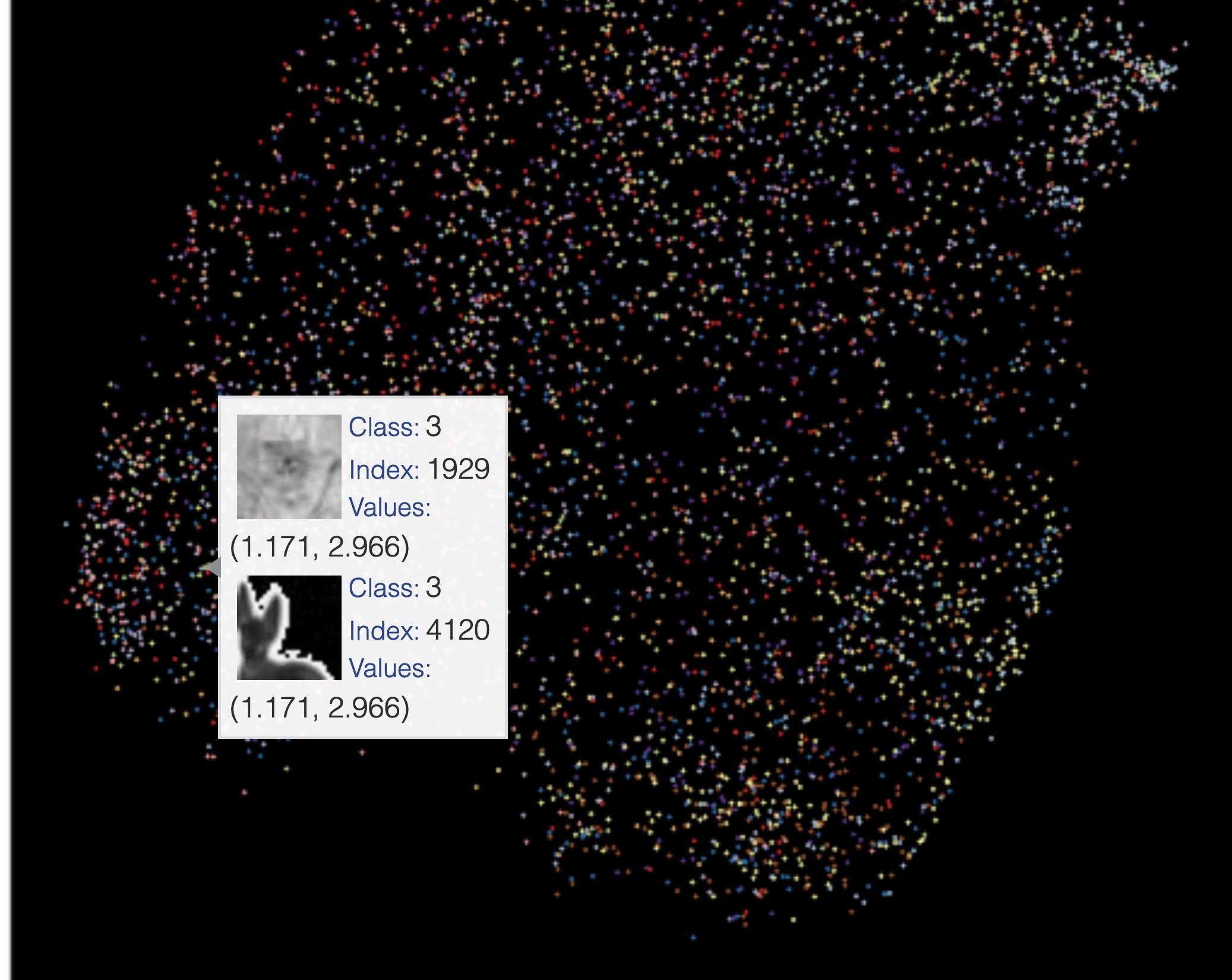Results of CIFAR image feature visualization using UMAP showing samples of cats that are reprojected into the same located in the embedded space. (Image provided by author)

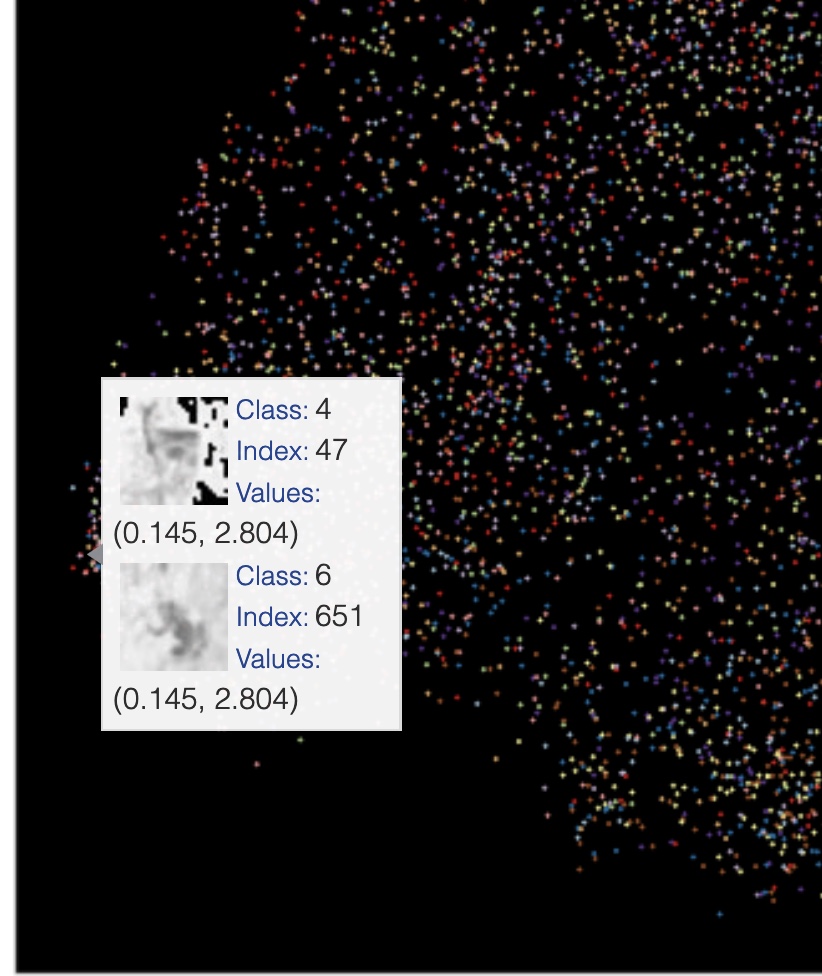Likewise, if we look at the following figure where deer and frog are co-located in embedded space, we can see the image texture is very similar. This texture however is the result of normalization and grayscale conversion. As we can see, a lot goes on in nature scenes and without a clear understanding of which features to focus on, one's features can be other's noise.

Results of CIFAR image feature visualization using UMAP. Shows images in an overlay on randomly selected points. (Image provided by author)

t-SNE and UMAP are feature visualization techniques and perform best when the data vector represents the feature sans noise.

What to do when there is noise in features?

So, what can we do if there are noises in our feature vectors? We can apply techniques that reduce noises from feature vectors before applying manifold learning algorithms. Given the emphasis on nonlinearity in both t-SNE and UMAP (to preserve nonlinear features), it is better to choose a noise reduction technique that is nonlinear.

Autoencoder is a class of unsupervised deep learning techniques that learns the latent representation of the input dataset eliminating noises. Autoencoder can be non-linear depending on the choices of layers in the network. For example, using a convolution layer will allow for non-linearity. If noises are present in the feature vector then an autoencoder can be applied to learn latent features of a dataset and to transform samples to noise-free samples before applying manifold algorithms. UMAP has native integration with Tensorflow for similar use cases that is surfaced as parametric UMAP. Why parametric because autoencoders/neural networks are parametric! i.e. increasing data size will not increase parameters - the parameters may be large but will be fixed and limited. This approach of transforming input feature vectors to the latest representation not only helps with noise reduction but also with complex and very high dimensional feature vectors.

The following figure shows the results of applying autoencoder before performing manifold algorithm t-SNE and UMAP for feature visualization. As we can see in the result, the clumps are much more compact and the gaps are wider. The proximity of MNIST classes remains unchanged, however - which is very nice to see.

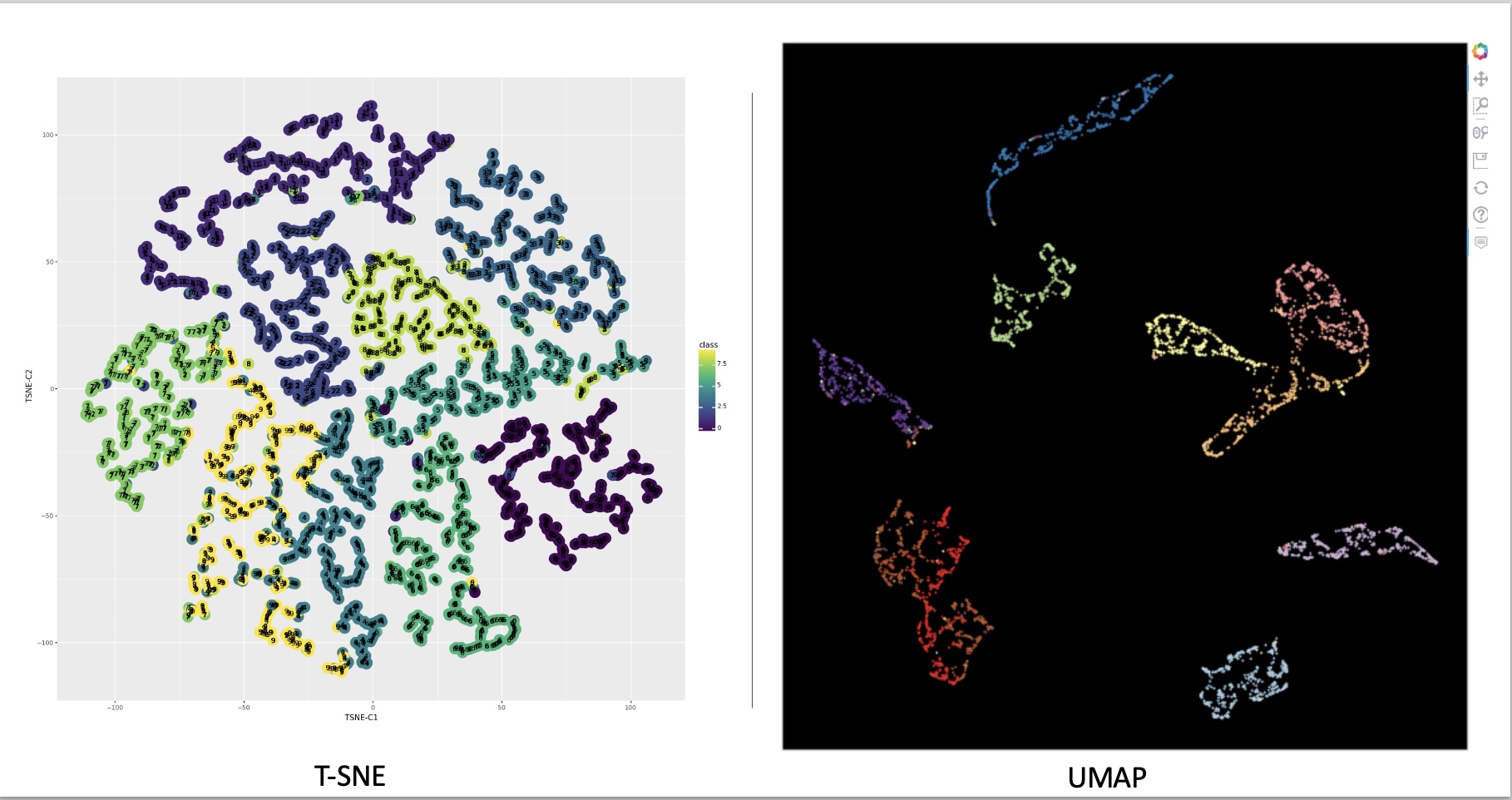Results of applying autoencoder on MNIST before applying manifold algorithm t-SNE and UMAP. (Image provided by author)

So how does it affects the features that contribute to proximities/neighborhood of data? The manifold algorithm is still the same however it's now applying on latent feature vector as produced by autoencoders and not raw features. So effectively, the proximity factor is now calculated on latent representation and not directly on perceptible features. Given the digit clusters are still holding global structure and it's just more packed together within the classes, we can get the sense that it's doing the right things if intra-class clumps can be explained. Let's look at some examples. The following shows a reprojection in the embedded space where 4,9 and 1 are clustered together into larger clusters of 1s. If we look closely the backbone of all these numbers is slanting at about 45 degrees and perhaps that has been the main driving factor. The protruding belly of 4 and 9 are largely ignored but also they are not very prominent.

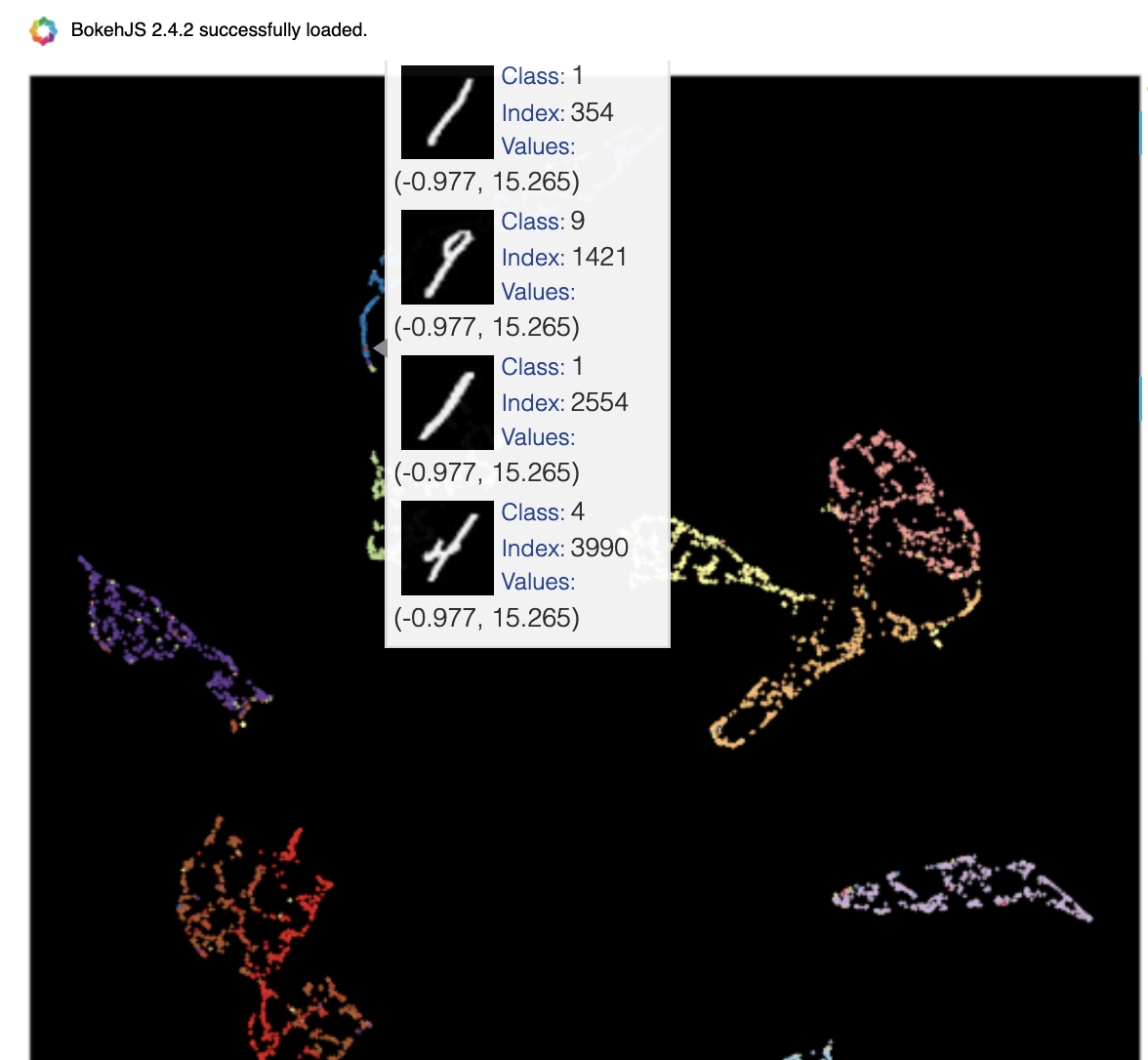Example of co-located 1s, 4 & 9 in embedded space obtained by applying Paramertic UMAP on MNIST. (Image provided by author)

More importantly, looking at the dataset (in the following figure), there are not as many 9s or 4s that have a backbone at that steep slant of 45 degrees. This is more easily shown in the full-scale overlay in the following figure (sparsely chosen images to show to make it more comprehensible). We can see all samples are upright 4s and 9s where there is a slant the protrusion is more prominent. Anyhow, we don't need to get overboard with this as manifold algorithms are not feature detection algorithms and certainly can't be compared to the likes of more powerful feature extraction techniques like convolution. The goal with manifold is to find global and local structures in the dataset. These algorithms work best if signals in datasets are noise-free where noise includes features/characteristics we want ignored in the analysis. A rich natural background is a very good case of noise as shown already in the CIFAR case.

Images overlaid on t-SNE of auto-encoded features derived from MNIST dataset. (Image provided by author)

how to do this for multi-label

In the early day of learning about this, I found myself wondering how would we do the feature analysis on a multi-label dataset? Multi-class is certainly the easy case - each sample only needs to be color-coded for one class so is easy to visualize. We are also expecting class-specific data to be clumped together mostly (perhaps not always and depends on intent but may be more commonly).

If multi-label data consists of exclusive classes similar to Satnford Cars Dataset where options within the make and the models of cars are mutually exclusive, then splitting the visualization to the group of exclusive cases could be very helpful.

However, if the multi-label dataset is more alike MLRSNet where classes are independent then it's best to first analyze the data class agnostic and explore if there are any patterns in features and proceed based on this.

Can we apply this to understand what neural networks are doing?

A lot of work has been done in the area of explainability and feature understanding that is very well documented in distill blogs. The underlined idea is that we can take the activation of the layers of the neural network and explore what features it is that that particular layer is paying attention to. The activations are essentially the signal that is fired for a given input to the layer. These signals then formulate the feature vector for further analysis to understand where and what the layer is paying more attention to. T-SNE and UMAP are heavily used in these analyses.

The distill blogs are very well documented and highly recommended for reading if this is something that is of interest to you.

Conclusion

This post was focused on the fundamentals of manifold learning algorithms, and diving into the details of t-SNE and UMAP. This post also compared and contrasted t-SNE and UMAP and presented some analysis of MNIST and CIFAR datasets. We also covered what to do if we have a very high dimensional dataset and also if we have noises in the dataset. Lastly, we touched on what to do if your dataset is multi-label.

In the follow-up, I will cover how we can utilize t-SNE and UMAP to better understand what neural networks are doing and apply it in conjunction with convolutions as feature extractors.

[umap_doco] https://umap-learn.readthedocs.io/en/latest/how_umap_works.html

Reading book list

This list includes books that a) I have truly enjoyed reading and highly admire or b) Eagerly looking forward to reading. It has six sections:

  • Abstract Programming/AI
  • Kubernetes
  • Machine Learning, AI, Deep Learning
  • Statistics
  • Parenting
  • Miscellaneous

1. Abstract Programming

Real-World Bug Hunting Authored by Peter Yaworski

Code: The Hidden Language of Computer Hardware and Software Authored by Charles Petzold

The Pragmatic Programmer: your journey to mastery Authored by Andrew Hunt, David Thomas

Coders at Work: Reflections on the Craft of Programming Authored by Peter Seibel

The Book of Why: The New Science of Cause and Effect Authored by Judea Pearl

Clean Code Authored by Robert C. Martin

2. Kubernetes

Kubernetes: Up and Running Authored by Kelsey Hightower, Joe Beda, Brendan Burns

*Kubernetes Security Authored by Michael Hausenblas, Liz Rice *

*Container Security Authored by Liz Rice *

Kubernetes for Developers Authored by Joseph Heck

3. Machine Learning, AI, Deep Learning

The Quest for Artificial Intelligence: A History of Ideas and Achievements Authored by Nils J. Nilsson*

[Machine Learning: A Probabilistic Perspective] Authored by Kevin P Murphy

Neural Networks and Deep Learning Authored by Michael Nielsen

[Deep Learning] Authored by Ian Goodfellow et al.

[Machine Learning Yearning] Authored by Andrew Ng

4. Statistics

Linear Algebra Done Right, Authored by Sheldon Axler

Mathematical Statistics and Data Analysis, Authored by John A. Rice

Elements of Statistical Learning, Authored by Trevor Hastie et al.

Introduction to Statistical Learning Authored by Trevor Hastie et al.

5. Parenting

Becoming Brilliant: What Science Tells Us About Raising Successful Children Authored by Roberta Golinkoff, Kathryn Hirsh-Pasek

Thinking Parent, Thinking Child: Turning Everyday Problems into Solutions Authored by Myrna B. Shure

The Psychology of Babies: How relationships support development from birth to two Authored by Lynne Murray

6. Miscellaneous

The End of Ice: Bearing Witness and Finding Meaning in the Path of Climate Disruption Authored by Dahr Jamail

The Second Kind of Impossible: The Extraordinary Quest for a New Form of Matter Authored by Paul Steinhardt

[Machine Learning: A Probabilistic Perspective]: https://www.amazon.com.au/Machine Learning-Probabilistic-Kevin-Murphy/dp/0262018020

[Machine Learning Yearning]: https://www.deeplearning.ai/Machine Learning-yearning/

[Wikipedia ML dataset]: https://en.wikipedia.org/wiki/List_of_datasets_for_Machine Learning_research

[Hackernoon Rare dataset]: https://hackernoon.com/rare-datasets-for-computer-vision-every-Machine Learning-expert-must-work-with-2ddaf52ad862